Bleichenbacher Chosen Ciphertext Attack
Exploiting an RSA PKCS #1 v1.5 Padding Oracle
The Bleichenbacher attack established the first practical Adaptive Chosen Ciphertext Attack (CCA2) and defeated SSL v3.0 by exploiting PKCS #1 v1.5 padding "errors" under RSA. More specifically, the attack uses a Padding Oracle to identify messages with valid padding among a large set of attacker-generated messages. Each attacker-generated message with valid padding reveals a bit more about the original message - eventually allows the attacker to recover the plaintext without the secret key.
Public Key Cryptography Standards #1 v1.5
PKCS #1 v1.5 defines the padding applied to messages for minimizing crib material (known plaintext). Under PKCS #1 v1.5, a pseudorandom non-zero padding string (PS) is generated of at least 8-bytes and prefixed to the plaintext (P) as follows: 0x00, 0x02, PS, 0x00, P. The Padding Oracle will identify if a given ciphertext decrypts to that structure correctly (a so called conforming message), revealing that the decrypted ciphertext starts with 0x00, 0x02.
RSA Malleability
RSA relies on the difficulty of prime factorization for very large prime numbers, but the mathematical properties of RSA also make encrypted messages rather malleable. Given the public exponent E and public modulus N, a plaintext message M is encrypted into ciphertext C such that C = M^E (mod N). A modified ciphertext C' may be generated by applying a random integer S such that C' = C * S^E (mod N) which creates a related message M' such that M' = M * S (mod N).
Bleichenbacher Attack
A conforming ciphertext means that the plaintext value is between 0x0002 * B <= P < 0x0003 * B where the message_length B is (2^(8*(sizeof(N)-2))). If an integer S is found such that C' is conforming, then the bounds around P can be shrunk using 0x0002 * B <= P * S (mod N) < 0x0003 * B. An attacker can repeatedly find new integers that generate conforming messages, progressively tightening the bounds, until P is fully defined (e.g. x <= P < x+1 => P=x). This process is described in step 3:
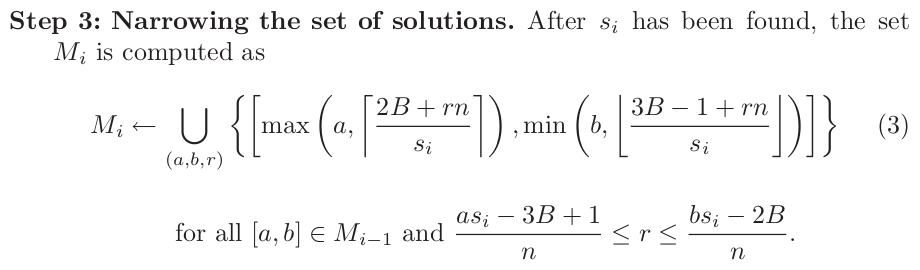
In other words, for all (a,b) from the last bounds and integers R (a*Si-3*B+1)/N <= R <= (b*Si-2*B)/N generate new bounds [max(a,(2*B+r*n)/Si),min(b,(3*B+r*n-1)/Si]. Per step 4, if any of thoe bounds are width 1 (e.g. [x,x]) then we've found the answer (P=x if S0=1 else P=x*modular_inverse(S0,N) mod N). Otherwise repeat until the bounds coalesce.
Full Python implementation available on Github